QOJ4892 难度 2

一条限制相当于要求 $a_i,a_j,a_k$ 的中位数为 $x$，这又等价于 $a_i,a_j,a_k$ 中至多一个数 $<x$，至多一个数 $>x$。

2sat，建出 $nV$ 个点 $(i,j)$ 表示 $a_i\le j$ 是否成立，其中 $1\le i\le n,1\le j\le V$，$V$ 是值域。

如果要求 $a_i,a_j,a_k$ 至多一个 $<x$，至多一个 $>x$，那就连边 $a_i<x\Rightarrow \text{not }a_j<x,a_i<x\Rightarrow \text{not }a_k<x$，等等。然后跑一个 2sat。注意有用的点只有 $O(m)$ 个，只保留这些点即可。

时间复杂度 $O(n+m)$。

QOJ7987 难度 2

考虑对一个 $k$ 算答案，我们把序列每 $k$ 个分一段，那么下一段可以由上一段递推得到。

具体来说，我们每次相当于把当前段复制到下一段，然后把下一段 $1$ 的位置那里 OR 一下，$0$ 的位置 AND 一下。这样每次需要进行 $O(n/k)$ 次长度为 $k$ 的 bitset 操作，每次操作复杂度是 $O(w+\frac{k}{w})$，于是总复杂度 $O(\frac{n^2}{w}+nw\log n)$。

Luogu9521 难度 3

考虑一个 $L_a\times L_b$ 的矩形，横着的两条边边权上下分别为 $a_1,a_2$，竖着的左右分别为 $b_1,b_2$，那么可以发现我们比的是 $a_1\times L_a+b_2\times L_b$ 和 $a_2\times L_a+b_1\times L_b$。做差得到

也就是说，如果 $a$ 那边的斜率更大，那么就应该先横着走；否则就竖着走。

这也就是说，最优解中的每一条折线，都应该满足，他先走的是斜率小的那一侧。

此时有一个 $O((n+m)\log (n+m))$ 的做法：每次找到全局最大的差分位置，然后消掉所有不可能的拐点。这样最后路径只会剩下一条，用 std::set 维护即可。官方题解里有详细的图解。

事实上，考虑三个点 $(i,a_i),(j,a_j),(k,a_k)$，如果他们不形成下凸，那么 $i,j$ 之间的斜率比 $j,k$ 之间要小，也就是说如果我们某一步选择了先走 $i\to j$ 那么一定会立刻走 $j\to k$，于是我们可以直接把路径缩成 $i\to k$。于是只需要求出 $a,b$ 的下凸壳，每次走斜率小的一边即可。复杂度 $O(n+m)$。

Luogu5972 难度 3

考虑从前往后 DP，暴力是记录 $S$ 表示目前选择的数的集合，这样状态数仍然是 $O(2^n)$ 级别。

但我们注意到，设 $i$ 后面的数分别为 $x_1,x_2,\cdots,x_k$，我们只关心 $[1,x_1),(x_1,x_2),\cdots,(x_k,n]$ 这些每一段中选了多少个数。于是状态数不会超过每段长度 $+1$ 的乘积，由柯西不等式可以知道一定在段长相同时取到最值，直接看成连续的情况来分析，简单求导可以得到最值在 $e^{n/e}$，由于问题是离散的于是最值大约是 $\max(2^{n/2},3^{n/3})$。

于是直接 DP 就可以了。时间复杂度是 $O(n^23^{n/3})$，使用 map 或许会被卡常，手写哈希表可以稳过。

Luogu11235 难度 3

注意到只需要处理所有合法区间的答案，而它们要么不交要么互相包含。于是可以对合法区间建出一棵树，设 $f(u,j)$ 表示只考虑 $u$ 代表的区间，保留 $j$ 个数所能达到的最大总和。那么首先有 $f(u,2)\leftarrow a_{l_u}+a_{r_u}$，然后我们需要对 $u$ 的若干儿子做 max+ 卷积，最后整体加上那些一定存在的数，也就是做一个整体偏移。

由于我们只关心 $\frac{f(u,j)}{j}$ 的 max，考虑有三个点 $A,B,C$，坐标分别为 $(x_A,y_A),(x_B,y_B),(x_C,y_C)$，不妨设 $x_A<x_B<x_C$，如果这三个点不形成上凸，那么可以证明 $A,C$ 至少一个比 $B$ 优。

于是我们只需要维护上凸壳上的点，合并时做 max 卷积直接维护闵可夫斯基和即可。这里为了能算出每个点的答案，可能不能简单地只维护凸包上的每条边，需要用平衡树维护整个凸壳上面的点来支持快速算前缀和的操作。

时间复杂度 $O(N\log^2N+Q)$。

Luogu11236 难度 3

考虑一个 $f$ 怎么算，把序列划分为相同数的极长连续段 $(x_1,c_1),(x_2,c_2),\cdots,(x_k,c_k)$，其中 $x_i$ 是第 $i$ 段的值，$c_i$ 是第 $i$ 段的元素个数。每次我们找到序列中的所有最小值，显然把它们缩起来一定不劣。

分类讨论一下，如果 $c_i$ 是偶数，那么直接缩成 $(x_i+1,\frac{c_i}{2})$；否则这个 $(x_i,c_i)$ 左右一定不可能发生合并了，它们互相独立，于是我们可以把 $(x_i,c_i)\to (x_i+1,\frac{c_i-1}{2}),(-1,1),(x_i+1,\frac{c_i-1}{2})$，这里 $-1$ 表示一个分隔符，它的左右互相独立。

这样每次缩完 $a$ 中的 min（这个 min 不算 $-1$）都至少 $+1$，于是最多进行 $O(\max a_i)$ 轮所有数就都相等了。这样我们可以在 $O(n\max a_i)$ 的时间内算出一个 $f$。

考虑区间询问怎么做，事实上我们发现只要 $x_i<\min(x_{i-1},x_{i+1})$，我们就一定必须得把 $(x_i,y_i)$ 化简一下。于是考虑线段树维护每个区间这样缩完之后变成什么样子即可。可以发现这样一直缩下去最终每个区间只会剩下左右两侧的各 $O(A_i)$ 个段，以及中间可能被阻断的若干段。中间那些段显然不会再造成贡献了，只需要记录他们的 max；合并的时候处理一下是否出现新的段即可。

时间复杂度 $O(A(N+Q\log N))$。$A=10$ 是值域。

LOJ4000 难度 3

考虑建一个 DFS 树，那么非树边都是返祖边。

考虑 $(u,v)$ 这样一条非树边，这里 $u$ 是 $v$ 的祖先。在删掉 $u$ 和 $v$ 之后图长这样：

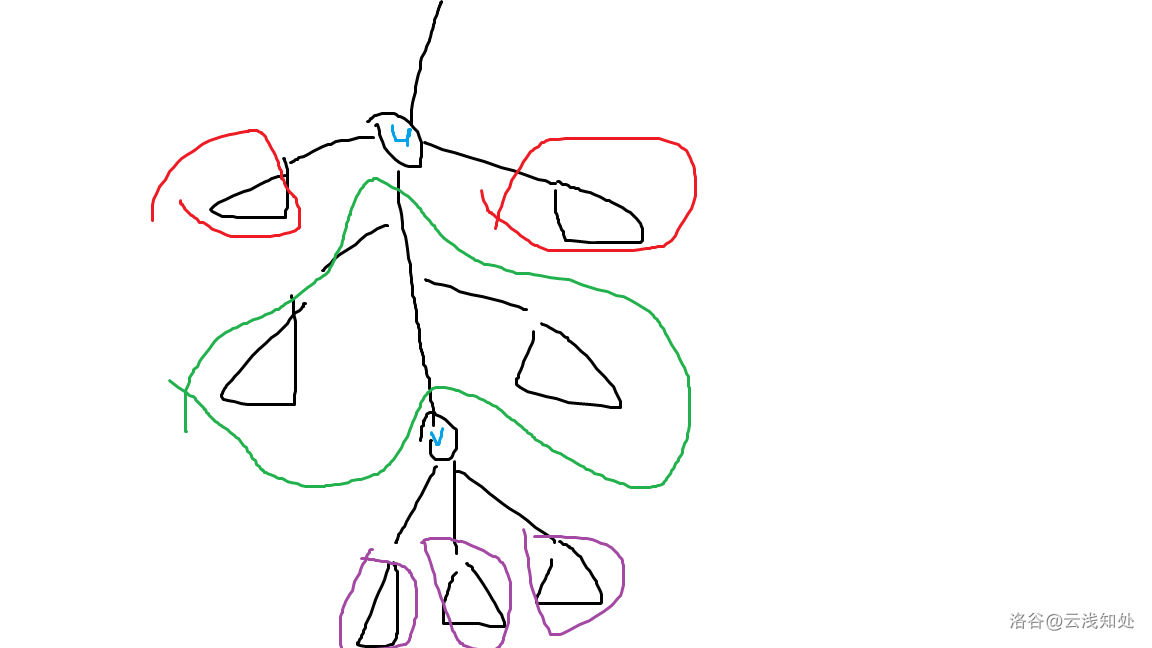
这里紫色部分和红色部分都可能不存在，但由于我们限定这是一条非树边因此绿色部分一定存在。$u$ 上面的部分也可能不存在，但稍后我们会看到这并不影响判断，

首先红色部分必须存在向上的连边否则就会和绿色部分分开。因此我们可以把红色部分和 $u$ 上面的部分看作一个整体。当 $u$ 为根节点的时候红色部分不存在，不过这不会影响我们的判断。

注意到绿色部分也是一个整体的连通块，紫色部分会构成若干连通块。那么紫色部分的每个子树要么和绿色部分有连边，要么和红色部分（指的是 $u$ 上面那部分）有连边（且红色部分存在）。我们分几类情况讨论：

• 存在一个紫色的子树和红绿均无连边：这个子树会被分割为独立的一个连通块，一定不合法。
• 存在一个紫色的子树同时和红绿均有连边（且红色部分存在）：（在判掉上面那种情况的前提下）一定合法。
• 每个紫色的子树都只和红色或绿色中的一个连边：这时需要绿色部分和红色部分有连边，或者红色部分不存在。

考虑三种情况怎么判，发现只需要维护某个子树内最浅和最深的一条返祖边，可以用线段树合并或启发式合并求出。对于第三种情况，绿色部分可以写成 DFS 序上的 $O(1)$ 个连续段，维护 DFS 序区间最小值即可。对于求出绿色部分顶端的点，发现本质上是树上 $k$ 级祖先。

接下来我们考虑树边怎么判。设 $u=fa_v$，有以下情况：

• $u$ 是根节点：如果 $u$ 在 DFS 树上的儿子数量 $\ge 3$ 一定无解，如果 $u$ 在 DFS 树上的儿子数量 $=2$ 那么要求 $v$ 在删去 $u$ 之后是一个孤立点。如果 $u$ 在 DFS 树上的儿子只有 $v$，那么这要求 $v$ 在 DFS 树上也只有一个儿子，或者 $v$ 是孤立点。
• $u$ 不是根节点：要求 $u$ 的除了 $v$ 的每个儿子都得有向上的连边，然后如果 $v$ 有儿子就必须连到 $u$ 的祖先上。

时间复杂度：$O(m\log n)$ 或 $O(m\log^2n)$。

ARC160E 难度 4

考虑删掉一个点 $i$，图中会出现 $\deg_i$ 个连通块；我们要求附加边能够将这些连通块连通起来。

显然，所有叶子都必须被连接。当叶子个数为偶数 $2k$ 的时候，我们设它们按照 DFS 序排序之后是 $p_1,p_2,\cdots,p_{2k}$，那么将 $p_i,p_{i+k}$ 配对一定合法。证明如下：

• 如果删掉二度点，由于子树内 DFS 序连续，因此 $p$ 会被分出来一个区间。显然按照我们这种连边方式，想要让两部分不连边，又得形成区间，必须得包含所有点。这显然不可能。
• 如果删掉三度点，那么 $p$ 会被分出来两段区间，和剩下一段补。考虑如果不连通，由于只有三个连通块，因此必然存在孤立的连通块。这样这个孤立的连通块必须包含所有点，也会导出矛盾。

考虑叶子个数是奇数怎么办。可以发现，只要保证删掉每个点后不存在孤立的连通块，方案就一定合法。钦定一个叶子 $x$ 不参与匹配，剩下的按照刚才的方法连边，那么这个时候想要在删掉一个点后出现孤立的连通块，只有一种可能：删掉这个点后，有一个连通块中仅包含 $x$ 这一个叶子节点。

我们发现这要求这个点到 $x$ 的路径上全都是二度点（当然这个点本身可以是三度点），而一个这样的点对 $x$ 的约束就是 $x$ 必须连到其他的子树上。发现只有和 $x$ 距离最近的一个三度点（显然是唯一的）能造成约束。

此时其实已经能做了，但我们再仔细考虑一下发现，任意一个点都一定能找到一个合法的这样的叶子，于是直接找非叶子中的最小权节点就行了。

ARC158F 难度 4

首先，对于相同的元素，由于稳定排序不改变相对次序，因此我们可以直接处理出来每个 $B_i$ 对应的是哪个 $A_j$。

回忆一下基数排序，发现是从低到高一位一位进行排序，这等价于按最高位为第一关键词，次高位为第二关键字，等等，进行排序。

考虑先后两次排序 $0\le i,j<K$，发现相当于按照第 $j$ 位为第一关键字，第 $i$ 位为第二关键字的排序。显然多次排序也是一样的，那么如果出现了 $i,j,i$ 这样的排序，相当于以 $i$ 为第一关键字，$j$ 为第二关键字，接下来应该是 $i$ 为第三关键字排序；但是 $i$ 本来就是第一关键字，因此前面那次排序是没用的。

因此，我们只需要考虑每一个位最后被排序的时刻，然后会得到一个 $0,1,\cdots,K-1$ 的排列（准确来说不一定是排列，某些元素可能根本没有出现过）。我们要做的就是对每个排列判断是否合法，再计算方案数。

枚举排列自然是不行的。首先考虑方案数怎么算，发现每一位等价，因此这个数只与排列大小相关；对于 $a$ 元的排列，他就等于最终恰好用到这 $a$ 个数的方案数除掉 $a!$。由容斥可得方案数为

• 实际上这就是第二类斯特林数。

对于排列的部分，考虑 $B$ 那边的限制实际上是啥。发现只需要最终 $B_i$ 在 $B_{i+1}$ 的左边。

如果 $B_i=B_{i+1}$，那么没有约束；否则考虑所有 $B_{i,x}\neq B_{i+1,x}$ 的位 $x$（这里记 $B_{i,x}$ 表示 $B_i$ 在十进制下的第 $x$ 位），把他们分为 $B_{i,x}<B_{i+1,x}$ 与 $B_{i,x}>B_{i+1,x}$ 的两个集合 $S,T$，那么对任意 $x\in T$，$x$ 的关键字次序前面必须排一个 $y\in S$ 的 $y$；如果 $S=\varnothing$，那么就不能有这样的 $x$。此外，如果原序列中 $B_i,B_{i+1}$ 的次序和现在这个序列不一样，那么至少要进行一次 $x\in S$ 的排序。

接下来就可以状压了。从高优先级的关键词往低优先级的关键字填，$f(S)$ 表示填完 $S$ 的方案数。那么接下来能填 $x$ 当且仅当对每个 $x$ 的约束 $T$，均有 $S\cup T\neq \varnothing$。那么不能填 $x$ 就当且仅当存在 $x$ 的约束 $T$ 使得 $T\subseteq U-S$。对每个 $x$ 做高维前缀和即可，复杂度 $O(K^22^K)$。

总复杂度 $O(N\log N+NK+K^22^K)$，三部分分别是求对应次序，处理约束，高位前缀和及状压 DP。

Luogu4117 难度 5

分块。我们先来考虑修改对整块的影响。记值域为 $V=10^5$。

考虑对每一块维护 $V$ 个集合 $S_1,S_2,\cdots,S_V$，第 $i$ 个集合 $S_i$ 维护了区间中所有 $=i$ 的元素的一些信息，并维护区间的最大值 $m$，对于一次操作 $x$：

• 若 $m\le 2x$，我们暴力对每个 $i\in [x+1,m]$，将 $S_i$ 合并进集合 $S_{i-x}$。
• 若 $m>2x$，那么操作相当于先把 $\le x$ 的数 $+x$，再做全局 $-x$。我们对每个 $i\in[1,x]$，把 $S_i$ 合并进 $S_{i+x}$，然后再给这个块打上标记 $x$，表示这个块实际上的 $=i$ 的元素构成的集合应该是 $S_{i+x}$。

我们设一次合并的复杂度为 $O(f(n))$，那么对于第一种情况，我们用 $m-x$ 次操作使 $m$ 减小了 $m-x$；对于第二种情况，我们用 $x$ 次操作使 $m$ 减小了 $x$。由于 $m\le V$ 且 $m$ 单调递减，因此一块的复杂度不会超过 $O(V\times f(n))$，总的复杂度就不超过 $O(V\sqrt{n}\times f(n))$。

考虑应当怎样维护这样的集合的合并。注意我们需要在散块处进行重构，还需要应对查询，因此我们的 $S_i$ 应当满足：

• 由 $S_1,\cdots S_V$ 足以推出整个块的完整信息。
• 可以查询某个集合的大小 $|S_i|$。

那么只需要维护 $S_i=\{j|a_j=i\}$，即所有 $=i$ 的元素位置即可。具体实现的时候，我们可以一开始把所有相同的数全都连到最先出现的位置上，并记录每种元素第一次出现的位置；同时我们维护每种元素第一次出现时的值。也就是说，我们维护的块中，（实际的序列中）每种元素第一次出现的位置（在我们维护的序列中）的值应当是正确的。

那么一次操作假设要把 $x$ 合并到 $y$ 上面，我们就找到 $r_x,r_y$，讨论一下：

• 如果 $r_x$ 不存在那么什么都不用干。
• 如果 $r_y$ 不存在，那么我们令 $r_y\leftarrow r_x$，然后令 $\text{val}(r_x)\leftarrow y$，最后把 $r_x$ 置为 $0$。
• 否则我们找到 $r_x,r_y$ 中较小的那一个 $p$，令 $\text{val}(p)\leftarrow y$，把 $r_y$ 的父亲置为 $p$，并令 $r_x\leftarrow 0$。

实际上这里维护的或许不能说是并查集，这更像一个链表，只不过是树形结构的。

如果要重构一块，由于我们保证了 $i$ 的父亲在 $i$ 前面，从前往后扫就行了。

直接做或许需要记录每一块的 $r$ 序列，考虑把询问全部离线，对每一块分别考虑他对所有修改与询问的贡献即可。这样空间复杂度就是线性，可以通过 P4117。